Unit Circle Chart Radians – Trigonometry Sin Cos Tan : The circle known as “Unit Circle” that has radius of 1.
Here we will discuss easy method to learn about sin cos tan unit circle chart, angles and lengths.
This unit circle’s main objective is to simplify additional mathematical trigonometry (Sin, Cos, Tan) calculations.
What is the Unit Circle?
In trigonometry, the unit circle refers to a circle centered at the origin with a radius of 1 unit. By convention, angles are measured counterclockwise from the positive x-axis.
On the unit circle, the x and y coordinates at any point correspond to the cosine and sine of the angle subtended from the origin to that point. This allows the trigonometric functions to be defined geometrically based on the unit circle.
Features of the Unit Circle Chart
Unit circle charts summarize some important patterns and properties:
- The sine and cosine values repeat every 360° or 2π radians.
- Sine is positive in quadrants I and II, negative in III and IV.
- Cosine is positive in quadrants I and IV, negative in II and III.
- Tangent is positive in quadrants I and III, negative in II and IV.
- Special angles have fixed sine, cosine and tangent values.
- Values can be calculated for any angle measure.
Visualizing these properties on the chart makes them easier to remember.
Radians vs. Degrees on the Unit Circle
While degrees are more common in everyday usage, radians are preferred on the unit circle for mathematical ease. Reasons include:
- The full circle is 2π radians which simplifies identities and formulas
- Trig values for angles like π/4, π/3, π/2 are exact square roots
- Sine and cosine curves repeat smoothly every 2π radians
- Radians remove factors like π/180 that complicate calculations
- radians align naturally with calculus and other higher math topics
Working with radians makes working with the unit circle more convenient. But degrees are still helpful for conceptualizing fractional slice angles.
Unit Circle Chart in Radians & Degrees
Unit Circle Chart Radians means: The unit circle represent angle of 2π radians. It also is divided into 4 quadrants 90°, 180°, 270°, and 360° (in degrees) or π/2, π. 3π/2, and 2π (in Radians).
A circle having unit radius of one & its centre at the origin is called a unit circle.
When compared to other circles and curved forms, it has a distinct value.
Check out the image below for the unit circle with chart.
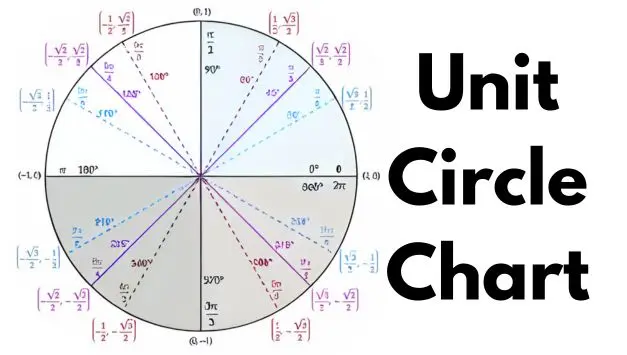
It is a circle of radius one, centred at the origin, and values (0, 0). The major use of this unit circle is to facilitate other mathematical operations.
In trigonometry, for example, the unit circle at any angle needs the values of cosine and sine. The values can be utilised with the unique sin (θ) = y and cos(θ) = x.
Certain angles have the same trig values at the centre point. unitcirclechart.com has further information on trig circle chart.
The half-unit circle is equal to 2π. It is a circular arc of equal length.
You may obtain it by measuring the angle that intersects this centre arc with a value of 2π since we know that the radius of the circle unit chart is one.
Unit Circle Radians Sin, Cos, Tan Table
| Angle θ | Unit Circle Radians | Sinθ | Cosθ | Tanθ = Sinθ/Cosθ | Coordinates |
|---|---|---|---|---|---|
| 0° | 0 | 0 | 1 | 0 | (1, 0) |
| 30° | π/6 | 1/2 | √3/2 | 1/√3 | (√3/2, 1/2) |
| 45° | π/4 | 1/√2 | 1/√2 | 1 | (1/√2, 1/√2) |
| 60° | π/3 | √3/2 | 1/2 | √3 | (1/2, √3/2) |
| 90° | π/2 | 1 | 0 | undefined | (0,1) |
Sine, Cosine, Tangent
When sin, cos, and tan are plotted on a graph, their measurements become visible.
Sin, Cos, Tan Unit Circle Chart at 0°
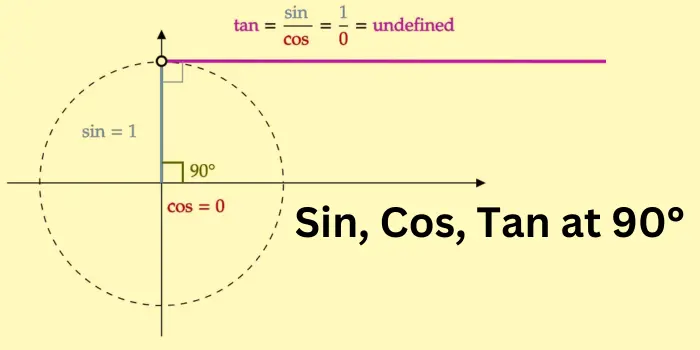
If the tangent start from x-axis on unit circle then Tan θ = 0.
- Sine (sin): sin(0°) = 0
- Cosine (cos): cos(0°) = 1
- Tangent (tan): tan(0°) = 0 (since tan(θ) = sin(θ) / cos(θ), and sin(0°) is 0, making tan(0°) / cos(0°) equal to 0)
Trigonometric Circle Chart Sin, Cos, Tan at 90°
At 90°, the tangent never reaches to the unit circle x-axis so, the tan(θ) is undefined.
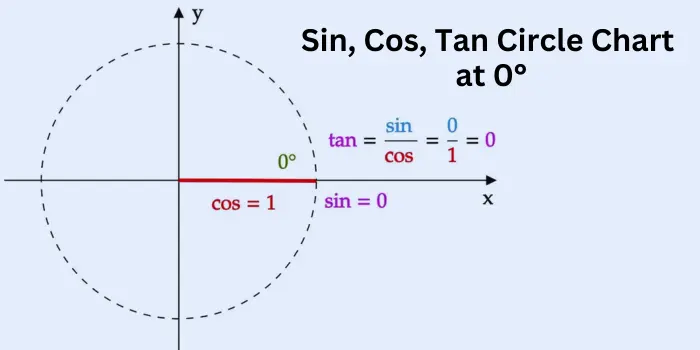
- Sine (sin): sin(90°) = 1
- Cosine (cos): cos(90°) = 0
- Tangent (tan): tan(90°) is undefined (since tan(θ) = sin(θ) / cos(θ), and cos(90°) is 0, making the division undefined)
Unit of Circle Chart Sin, Cos, Tan at 30 Degrees
- Sine (sin): sin(30°) = 1/2
- Cosine (cos): cos(30°) = √3/2
- Tangent (tan): tan(30°) = 1/√3 or √3/3
Sin, Cos, Tan at 45 Degrees Chart Unit Circle
- Sine (sin): sin(45°) = √2/2
- Cosine (cos): cos(45°) = √2/2
- Tangent (tan): tan(45°) = 1
Sin, Cos, Tan at 60 Degrees Circle Chart Trig
- Sine (sin): sin(60°) = √3/2
- Cosine (cos): cos(60°) = 1/2
- Tangent (tan): tan(60°) = √3
Because the radius of a unit circle is 1, it clearly displays trig functions. The values of sin, cos, and tan are unchanged by the hypotenuse.
Trigonometry Unit Circle Chart Ratios
There are several ratios in the unit circle chart. Each ratio has a unique set of values and functions. Sin, Sec, Tan, Cos, Csc, and cot ratios are shown on the chart.
If you want to readily analyse the while chart, you need also recall their functions. The ratios are as follows:
- sinθ = opposite/hypotenuse
- tanθ = opposite/adjacent
- cosθ = adjacent/hypotenuse
- cscθ = 1/sinθ
- cotθ = 1/tanθ
- secθ = 1/cosθ
4 Quadrants of Unit Circle Chart
The four quadrants of unit circle varies from 0-90°, 90°-180°, 180°-270° and 270°-360° degree or π/2, π. 3π/2, and 2π (in Radians).
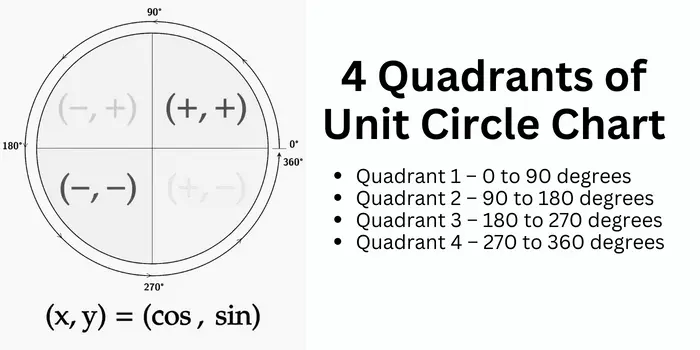
- Quadrant 1 – 0 to 90 degrees
- Quadrant 2 – 90 to 180 degrees
- Quadrant 3 – 180 to 270 degrees
- Quadrant 4 – 270 to 360 degrees
UNIT CIRCLE ANGLES IN UNIT CIRCLE CHART
The first side of the positive x-axis is used to measure the positive sides of a unit circle. You will then immediately proceed to the circle’s terminal side. The positive points are indicated in degrees and radians on the unit circle chart.
A straight line forms the construction of the circle angle’s terminal sides. These edge estimates include, for example, 30 and 210 degrees, 60 and 240 degrees, etc. The circle’s straight lines have a 180-degree value. You may determine the values of each angle in each of the four quadrants by analysing the trigonometry circle chart.
What is Radian Circle Chart?
The radian is a tool for measuring angles in any shape. A radian provides you with the precise angle you want in any design. The length of the radian is equal to the length of the circle arc.
The unit circle’s size and orientation are not important. For your knowledge, a complete circle has two radians, each having a value of 2π. Similarly, the radius value of π is equivalent to a half-unit circle.
What Are The Actual Values Of Sine, Cosine, And Tangent On Unit Chart Circle?
The actual values of sine, cosine, and tangent (sin, cos, tan) for the particular angles 30, 45, and 60 are displayed on unit circle chart.
- Sine (sin): The sine value is the y-coordinate of a point on the Unit Circle. At 0 degrees (or radians), sin(0) = 0; at 90 degrees (or π/2 radians), sin(90°) = 1; at 180 degrees (or π radians), sin(180°) = 0; at 270 degrees (or 3π/2 radians), sin(270°) = -1; at 360 degrees (or 2π radians), sin(360°) = 0.
- Cosine (cos): The cosine value is the x-coordinate of a point on the Unit Circle. At 0 degrees (or radians), cos(0) = 1; at 90 degrees (or π/2 radians), cos(90°) = 0; at 180 degrees (or π radians), cos(180°) = -1; at 270 degrees (or 3π/2 radians), cos(270°) = 0; at 360 degrees (or 2π radians), cos(360°) = 1.
- Tangent (tan): The tangent value is the ratio of sine to cosine. tan(θ) = sin(θ) / cos(θ). Note that tangent is undefined at 90-degree multiples (e.g., 90°, 270°) where cos(θ) = 0.
Cos and sin are the unit circle’s two centre coordinates. Keep in mind that a point in trigonometry can have any size, positive or negative.
How is the unit circle defined mathematically?
The unit circle is a circle centered at the origin on the Cartesian plane and with a radius of 1 unit. Angles are measured counterclockwise from the positive x-axis.
What are some tips for memorizing the unit circle chart?
Use mnemonics, make flashcards for key angles, practice questions using the values, and associate geometric positions on the circle with trig functions.
The unit circle chart is an indispensable learning aid for mastering trigonometry. Visualizing the circle geometry, coordinate positions, angle measures and function values builds intuitive understanding. Committing key parts of the chart to memory aids problem solving. As an elegant mathematical concept, the unit circle has significance even beyond trigonometry across science and engineering.